Study Shows Advances in High-Order Neural Networks for Industrial Applications

Table of Links

Abstract and 1. Introduction

2. Preliminaries and 2.1. Blind deconvolution

2.2. Quadratic neural networks

3. Methodology

3.1. Time domain quadratic convolutional filter

3.2. Superiority of cyclic features extraction by QCNN

3.3. Frequency domain linear filter with envelope spectrum objective function

3.4. Integral optimization with uncertainty-aware weighing scheme

4. Computational experiments

4.1. Experimental configurations

4.2. Case study 1: PU dataset

4.3. Case study 2: JNU dataset

4.4. Case study 3: HIT dataset

5. Computational experiments

5.1. Comparison of BD methods

5.2. Classification results on various noise conditions

5.3. Employing ClassBD to deep learning classifiers

5.4. Employing ClassBD to machine learning classifiers

5.5. Feature extraction ability of quadratic and conventional networks

5.6. Comparison of ClassBD filters

6. Conclusions

Appendix and References

2.2. Quadratic neural networks

The concept of high-order neural networks, also known as polynomial neural networks, has its roots in the 1970s. The Group Method of Data Handling (GMDH), which utilizes a polynomial network as a feature extractor, was first proposed by Ivakhnenko [42]. Subsequently, Shin and Ghosh [43] introduced the pi-sigma network to incorporate high-order polynomial operators:

where 𝑤, 𝑏 are learnable parameters, 𝜎(⋅) represents the activation function, and 𝑥 denotes the input. The high-order polynomials are implemented by multiplying several linear functions.

In recent years, advances in deep learning have provided a platform for re-examination and integration of polynomial operators into fully-connected neural networks and convolutional neural networks. Methodologies for introducing polynomials into neural networks can be categorized into two classes: polynomial structure and polynomial neuron. In terms of the former, polynomial neural networks were developed using polynomial expansion via recursion [44] or tensor decomposition [45, 46]. For the latter, the linear function (neuron) in traditional neural networks was substituted with various polynomial functions [34, 47]. This study primarily focuses on the neuron-level methods.

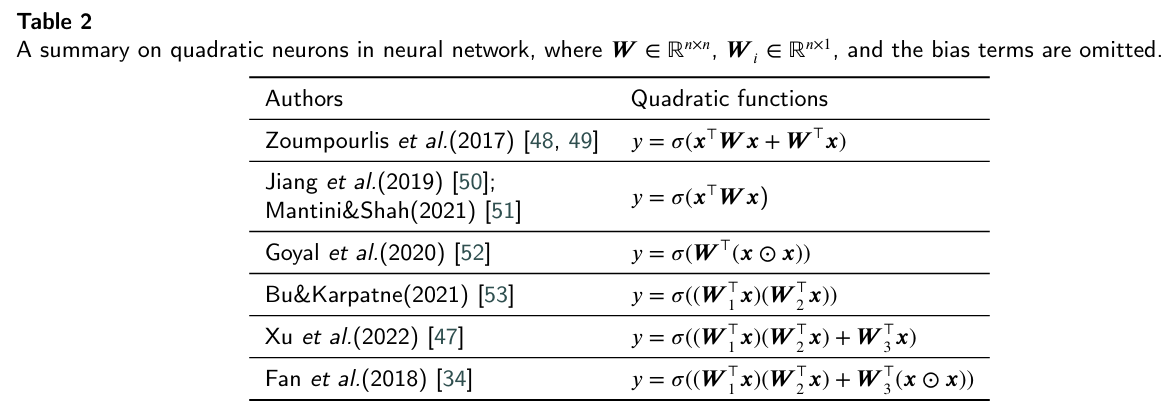
While polynomial functions can be extended to higher orders, this significantly increases the computational complexity of the neural network. To facilitate stable training, the polynomial function is typically restricted to the second order, which is known as quadratic neural network.

It is noteworthy that a variety of quadratic neurons have been proposed in the literature as summarized in Table 2. In this paper, we opt for the version proposed by Fan et al. [34] (see Eq. (7)). Compared the quadratic neuron proposed by Fan et al. and others (Bu&Karpatne, Xu et al.), it serves as a general version which consists of entire inner-product term and power term.