Researchers Develop Advanced Methods for Fault Diagnosis Using Blind Deconvolution

Table of Links

Abstract and 1. Introduction

2. Preliminaries and 2.1. Blind deconvolution

2.2. Quadratic neural networks

3. Methodology

3.1. Time domain quadratic convolutional filter

3.2. Superiority of cyclic features extraction by QCNN

3.3. Frequency domain linear filter with envelope spectrum objective function

3.4. Integral optimization with uncertainty-aware weighing scheme

4. Computational experiments

4.1. Experimental configurations

4.2. Case study 1: PU dataset

4.3. Case study 2: JNU dataset

4.4. Case study 3: HIT dataset

5. Computational experiments

5.1. Comparison of BD methods

5.2. Classification results on various noise conditions

5.3. Employing ClassBD to deep learning classifiers

5.4. Employing ClassBD to machine learning classifiers

5.5. Feature extraction ability of quadratic and conventional networks

5.6. Comparison of ClassBD filters

6. Conclusions

Appendix and References

2. Preliminaries

Table 1 presents some important symbols that will be used later in this paper.

2.1. Blind deconvolution

However, due to the complexity of machinery systems, it is often impractical to accurately estimate the transfer function and its frequency response. This challenge is further compounded by the presence of unpredictable noise. Consequently, in the absence of prior information, such as an accurate fault impulse period, BD is considered as an ill-posed problem. Given the non-stationary and periodic nature of the fault characteristics, a variety of sparsity indexes have been proposed to function as optimization objective functions [23, 24, 29, 39]. A representative example is kurtosis [27], which is utilized as the objective function in MED [26]:

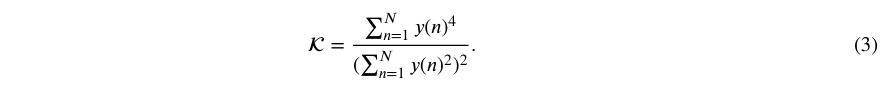
where 𝑦(𝑛) denotes the output of the BD filter, and its length is equal to the input 𝑁.

Essentially, Kurtosis is a statistical quantity that assesses the data distribution. An increase in the kurtosis value indicates a deviation from the standard normal distribution [27]. Intuitively, cyclic impulses emerge in the vibration signals when the fault occurs, and the kurtosis value of vibration signal gets increased due to the presence of more peaks (outliers). Consequently, maximizing kurtosis drives the adaptive filter to recover more impulses. Naturally, the optimization objective is defined as follows:

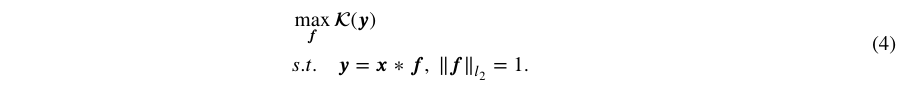
Several effective optimization methods have been developed for BD, including matrix operations [23, 26], particle swarm optimization (PSO) [32, 33], and backpropagation [40, 41]. Obviously, the performance of BD is strongly influenced by the choice of optimization method.In recent years, considerable efforts have been made to identify more general objective functions, design new filters, and devise more powerful optimization tools [2].